We R Live 13: Introdução à estatística espacial IV
GeoCast Brasil
Felipe Sodré M. Barros
Maurício Vancine
18/08/2020
We R Live 13
Tópicos
Introdução (40 min.)
1 Desafio da We R Live 13
2 Pacotes a serem usados
3 Considerações conceituais
- Dados agregados ou dados de área
- Alguns cuidados
- Análise exploratória
- Teste de correlação espacial (Indice de Moran I)
- 3.1 O que é
- 3.2 Vizinhança
- 3.3 Peso espacial
- 3.4 Lagging value (média móvel)
- 3.5 Cálculo Indice Global de Moran I
We R Live 13
4 Processamento de dados
group_by()summarise()
Mão na massa (30/40 min.)
O pulo do gato
5 Considerações finais (5 min)
Mas antes! Recados!!!
Recados
1. Apoie as iniciativas do GeoCast Brasil:
- Não deixe de curtir as lives e videos;
- Não deixe de se inscrever no canal;
- Ajude divulgando nas redes sociais;
2. Lives passadas: visite nosso site:
3. Dúvidas e sugestões: issues
1 Desafio da We R Live 13
1 Desafio da We R Live 13
Analisar estrutura de distribuição espacial dos votos no estado do RJ nas eleições de 2018
- Análise/teste de correlação espacial dos votos;
1 Desafio da We R Live 13
Analisar estrutura de distribuição espacial dos votos no estado do RJ nas eleições de 2018
- Análise/teste de correlação espacial dos votos;
Extras:
- Acessar dados da eleição de 2018;
- Usar funções do tidyverse, como:
group_by()summarize()
- Realizar joins tabulares e espaciais (já explorado na live 10)
1 Desafio da We R Live 13
Analisar estrutura de distribuição espacial dos votos no estado do RJ nas eleições de 2018
- Análise/teste de correlação espacial dos votos;
Extras:
- Acessar dados da eleição de 2018;
- Usar funções do tidyverse, como:
group_by()summarize()
- Realizar joins tabulares e espaciais (já explorado na live 10)
1 Desafio da We R Live 13
Base conceitual
2 Pacotes a serem usados
2 Pacotes a serem usados
Instalação
Instalar pacotes
install.packages(c("sf", "tidyverse", "tmap", "spdep"), dependencies = TRUE)2 Pacotes a serem usados
Instalação
Instalar pacotes
install.packages(c("sf", "tidyverse", "tmap", "spdep"), dependencies = TRUE)# Para instalar o cepesp-r - dados das eleicoesif (!require("devtools")) install.packages("devtools")devtools::install_github("Cepesp-Fgv/cepesp-r")3 Considerações conceituais
3 Considerações conceituais
Dados agregados ou dados de área
Os dados aglomerados ou dados de área (os famosos dados poligonais) possuem informações a respeito de uma determinada área do espaço geográfico.
Os limites desses poligonos podem ser definidos tanto pelo investigador (levando em consideranção o objeto de estudo), como um limite arbitrário ou, até mesmo, um limite administrativo criado com diferentes objetivos. Neles as informações associadas são frequentemente agregadas como, por exemplo, contagem populacional.
Nesses casos, não se pode saber exatamente como se dá a distribuição espacial do fenómeno estudado dentro do limite que o agrega.
3 Considerações conceituais
Alguns cuidados
A coleta de dados deve considerar a área de análise. Dessa forma, a inlfuencia do da escala será reduzida.
E quando se trata de análise temporal temos que tomar cuidado com o fato de que as áreas poderão ter sido alteradas com o passar do tempo. Para solucionar isso, se usa as áreas mínimas comparáveis (AMCs).
Por exemplo:
3 Considerações conceituais
Alguns cuidados
A coleta de dados deve considerar a área de análise. Dessa forma, a inlfuencia do da escala será reduzida.
E quando se trata de análise temporal temos que tomar cuidado com o fato de que as áreas poderão ter sido alteradas com o passar do tempo. Para solucionar isso, se usa as áreas mínimas comparáveis (AMCs).
Por exemplo:
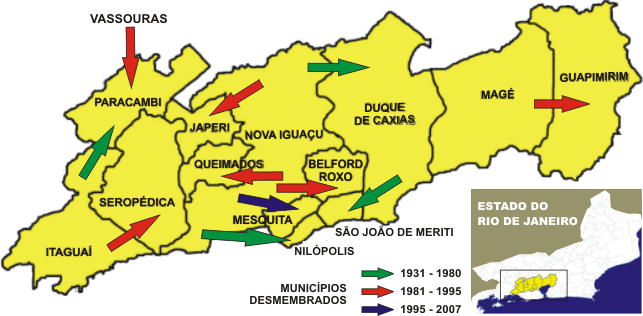
3 Considerações conceituais
Alguns cuidados
A coleta de dados deve considerar a área de análise. Dessa forma, a inlfuencia do da escala será reduzida.
E quando se trata de análise temporal temos que tomar cuidado com o fato de que as áreas poderão ter sido alteradas com o passar do tempo. Para solucionar isso, se usa as áreas mínimas comparáveis (AMCs).
Por exemplo:
O IPEA está trabalhando na elaboração desses dados para o Brasil e em breve estará disponível pelo geobr.
3 Considerações conceituais
Análise exploratória
A forma mais usual de explorar este tipo de dado é representando os mesmos em forma de mapas coropléticos (a.k.a "fazendo mapas bonitinhos"): Mapas coloridos representando a variação de determinado valor ou categoría em uma área de estudo que contém várias áreas amostrais (polígonos).
E é comum usarmos este tipo de mapa para tentar tirar conclusões sobre o padrão espacial do fenômeno.
Trata-se, como alerta Câmara et al., de uma abordagem meramente intuitivas/subjetiva. E que, para alguns casos, precisamos ir além.
3 Considerações conceituais
Teste de correlação espacial
Discernir visualmente o padrão de distribuição de determinado fenômeno não é uma tarefa óbvia, além de ter uma carga subjetiva elevada.
O teste de autocorrelação espacial se apresenta como uma abordagem estatística (quantitativa e objetiva) para identificar qual o padrão de distribuição espacial das informações relacionadas aos polígonos.
Vamos usar o Indice de Moran I (Moran's I test).
Para saber mais sobre os padrões de distribuição espaciais: (re)vejam a live #7.
3 Considerações conceituais
Indice de Moran I
3.1 O que é
O indice de Moran I é um coeficiente que informa se o valor de uma variável (como quantidade de votos para um candidato, riqueza de espécies, quantidade de pessoas afetadas por um virus, etc) em uma feição é correlacionada com os valores das feições vizinhas.
Com o indice global de Moran I, se tem a magnitude da autocorrelação espacial da variável estudada entre as áreas amostradas.
3 Considerações conceituais
Indice de Moran I
3.1 O que é
O indice de Moran I é um coeficiente que informa se o valor de uma variável (como quantidade de votos para um candidato, riqueza de espécies, quantidade de pessoas afetadas por um virus, etc) em uma feição é correlacionada com os valores das feições vizinhas.
Com o indice global de Moran I, se tem a magnitude da autocorrelação espacial da variável estudada entre as áreas amostradas.
Mas antes de realizar o tete, temos que pensar e discutir alguns conceitos fundamentais, como:
- Vizinhança;
- Peso espacial;
3 Considerações conceituais
3.2 Vizinhança
A definição de vizinhança é fundamental nesse tipo de análise, e deve ser considerado a natureza do fenômeno de estudo na definição do mesmo, já que há várias formas de definir os polígonos vizinhos:
- Por contiguidade;
- Queen case;
- Rook case;
3 Considerações conceituais
3.2 Vizinhança
A definição de vizinhança é fundamental nesse tipo de análise, e deve ser considerado a natureza do fenômeno de estudo na definição do mesmo, já que há várias formas de definir os polígonos vizinhos:
- Por contiguidade;
- Queen case;
- Rook case;
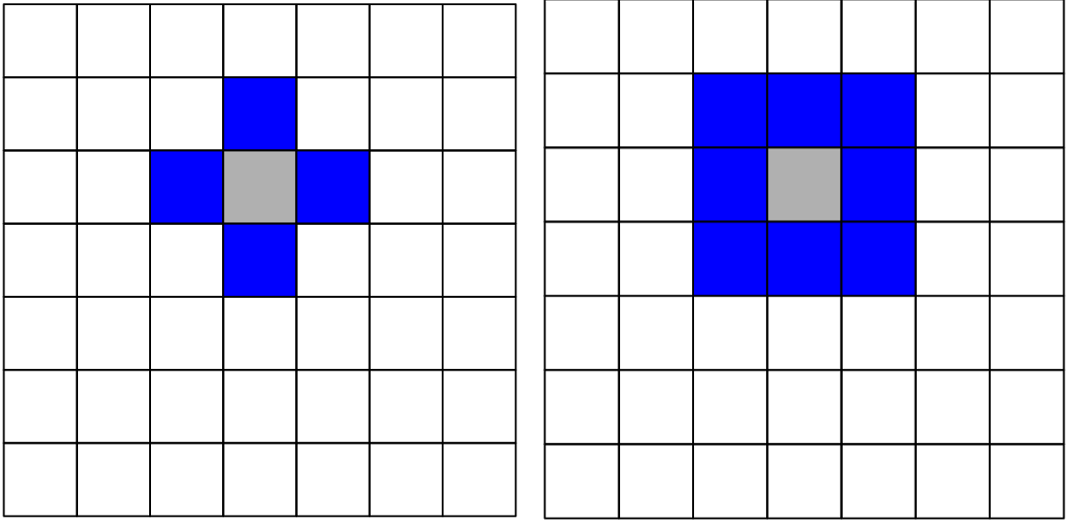
3 Considerações conceituais
3.2 Vizinhança
A definição de vizinhança é fundamental nesse tipo de análise, e deve ser considerado a natureza do fenômeno de estudo na definição do mesmo, já que há várias formas de definir os polígonos vizinhos:
- Por contiguidade;
- Queen case;
- Rook case;
3 Considerações conceituais
3.2 Vizinhança
A definição de vizinhança é fundamental nesse tipo de análise, e deve ser considerado a natureza do fenômeno de estudo na definição do mesmo, já que há várias formas de definir os polígonos vizinhos:
- Por contiguidade;
- Queen case;
- Rook case;
- Por distância;
- K Vizinhos mais próximos (k nearest neighbors);
Os métodos de vizinhança baseados em distância, em geral, usam o centroide do polígono para a estimação dos polígonos vizinhos e não o seu perímetro/vértices.
3 Considerações conceituais
3.2 Vizinhança
Contiguidade
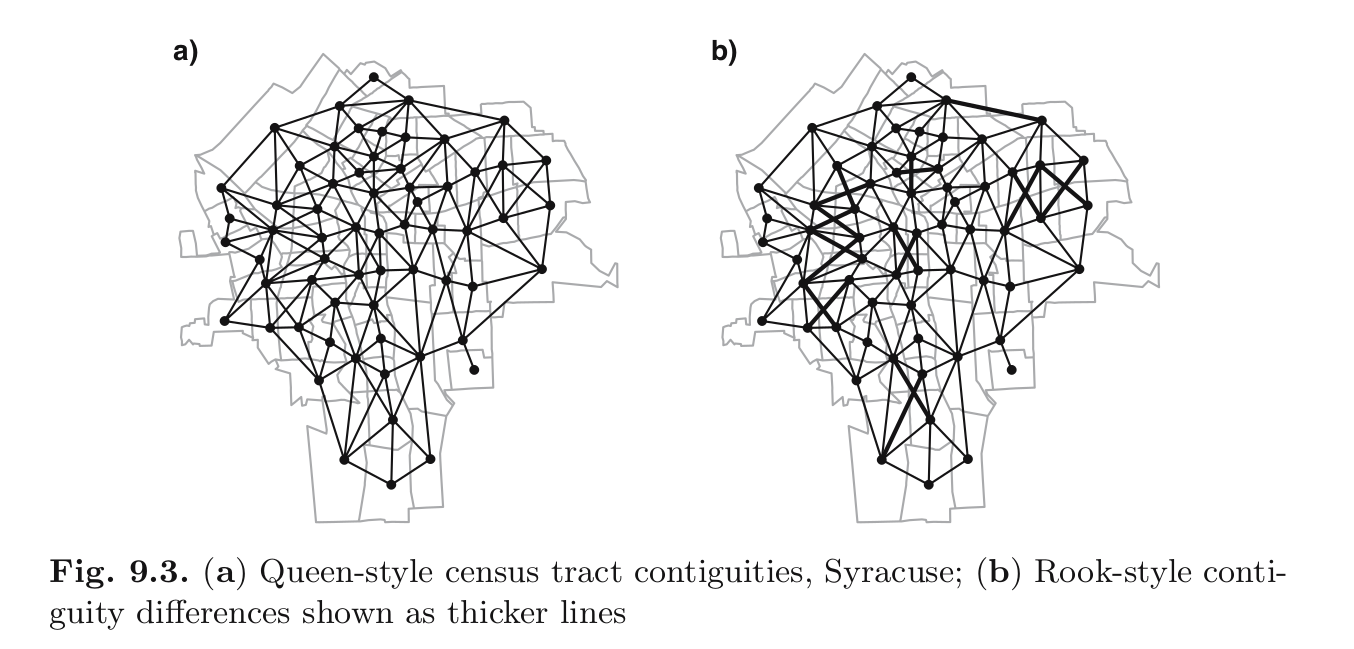
Fonte: Applied Spatial Data Analysis with R
3 Considerações conceituais
3.2 Vizinhança
Distância
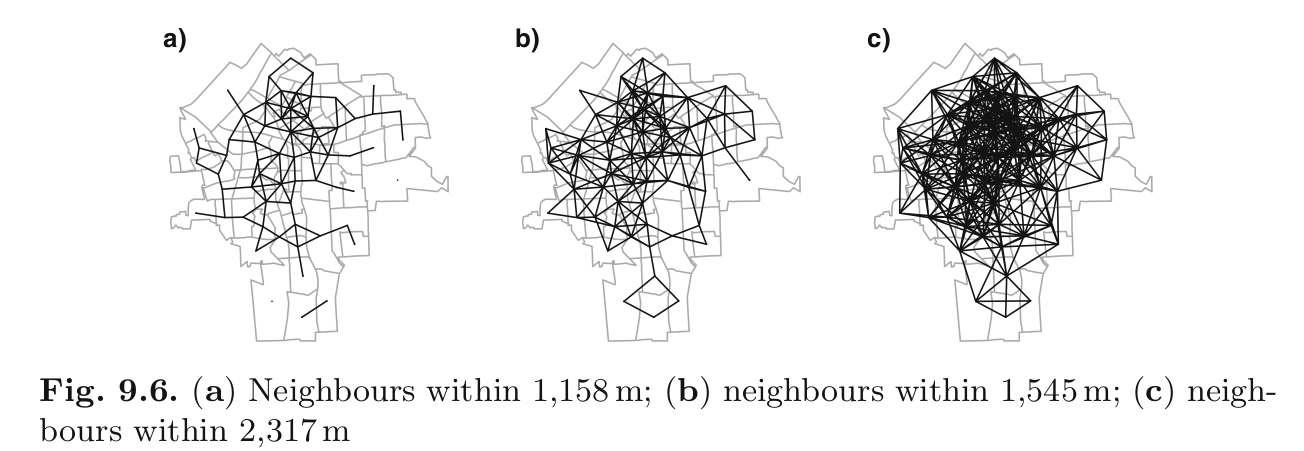
Fonte: Applied Spatial Data Analysis with R
3 Considerações conceituais
3.2 Vizinhança
K vizinhos mais próximos
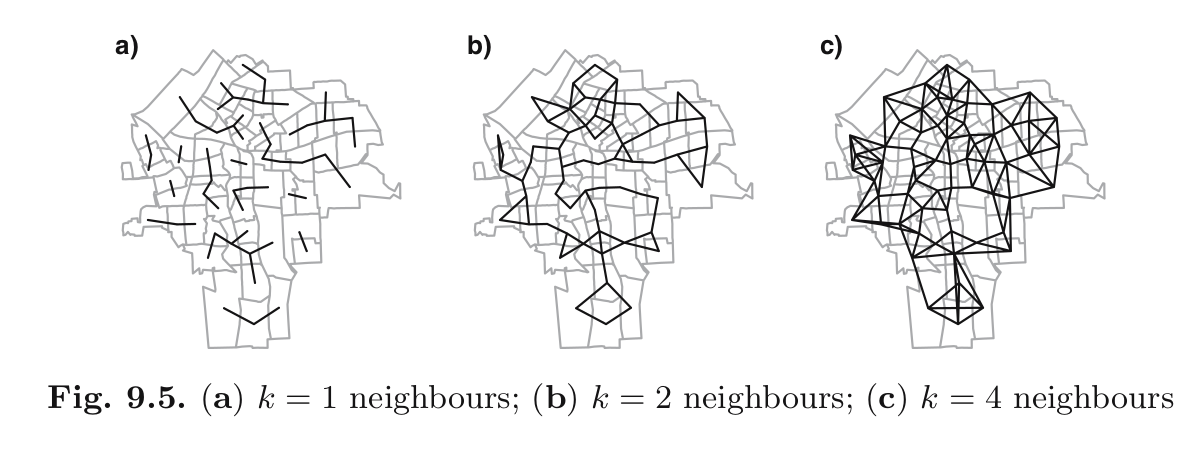
Fonte: Applied Spatial Data Analysis with R
3 Considerações conceituais
3.2 Vizinhança
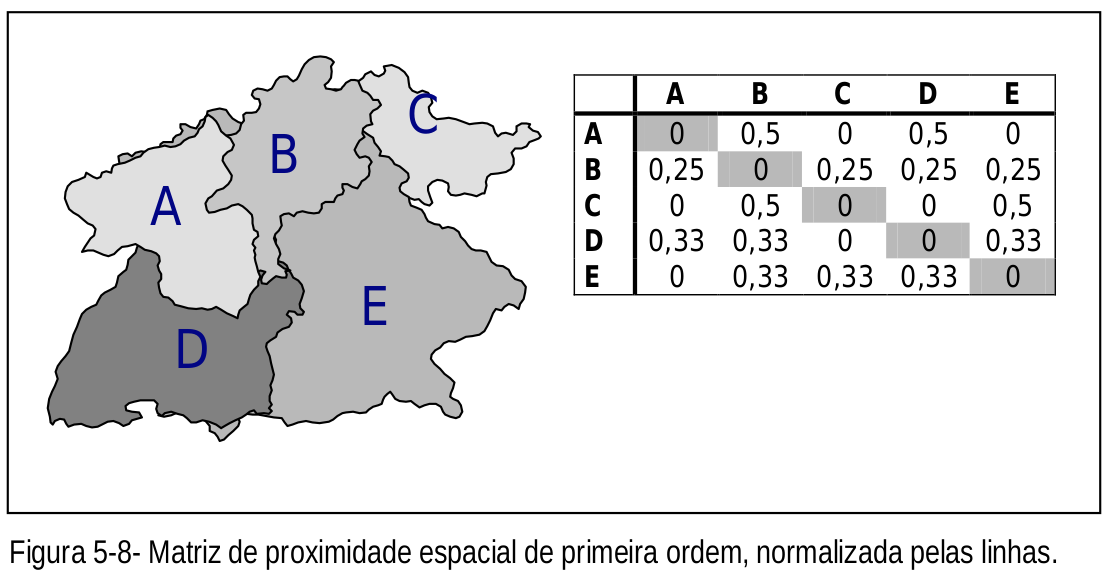
Uma vez definido o conceito de vizinhança a ser utilizado, pode-se construir a matriz de vizinhança, também chamada matriz de proximidade espacial ( wij ). Que estão será usada na análise de correlação espacial.
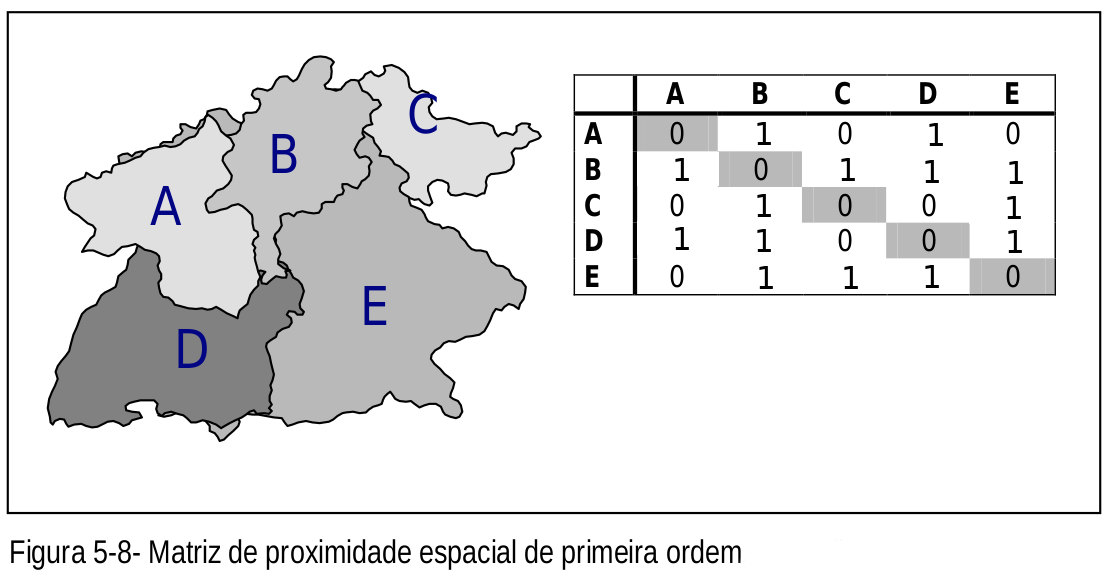
Fonte: Adaptado de Câmara et al.
Há a possibilidade de considerar vizinhança de segunda ou maiores ordens.
Um ponto a considerar é com relação aos polígonos que estejam no limite da área de estudo que, em geral terão menos polígonos vizinhos e com isso induzir a um viés de super ou sub estimação da correlação espacial.
3 Considerações conceituais
3.3 Peso espacial
Antes de seguir com a análise, precisamos definir o peso espacial ao qual podemos adotar algumas estratégias:
- Definir o mesmo peso a cada polígonos (style = "W") (mais intuitivo);
- O valor será definido pela fração 1#vizinhos;
- A cada vizinho é atribuido o valor ponderado pelo peso;
- Outras opções sariam:
- "B" definindo um valor binário para vizinhos e não vizinhos;
- Ver mais em
?nb2listw
zero.policy = TRUE: peso igual a zero é inserido para regiões sem vizinhos.
3 Considerações conceituais
3.4 Lagging value (média móvel)
Feita a identificação dos polígonos vizinhos e a definição do peso espacial, calcula-se um resumo dos valores dos polígonos vizinhos aglomerados (calculando, por exemplo seus valores médios), chamado de lagging value ou média móvel:
^μi=n∑j=1wijzi
No nosso trabalho, vamos adotar a estimativa de vizinhança por contiguidade e o peso ponderado pela quantidade de vizinhos ("W"), usando o percentual de votos para o PT como variável de análise.
3 Considerações conceituais
3.5 Cálculo Indice Global de Moran I
I=n∑i=1n∑j=1wij(zi−¯z)(zj−¯z)n∑i=1(zi−¯z)2
O indice de Moran I é um coeficiente que varia entre valores negativos e positivos (entre -1 e +1) indicando desde correlação inversa até correlação direta, sendo os valores zero a ausencia de correlação espacial.
Contudo, independente do resultado, precisamos identificar o nível de significância do mesmo.
3 Considerações conceituais
3.6 Cálculo de sginificância
O indice de Moran I, por si só, nos informa o valor obervado de correlação espacial. Para confirmar que este valor é significativo, devemos compará-lo com valores simulados segundo a hipótese nula (distribuição aleatória).
Para isso, vamos usar a simulação de Monte Carlo que usa os mesmos polígonos, ams atribui a eles valores aleatórios clculando o indice Moran I a cada simulação. Com isso, temos a distribuição dos valores de Moran I segundo a hipótese nula.
Essa dsitribuição é então comparada com o valor observado do teste Moran I.
Processamento de dados
4 Processamento de dados
Antes de meter a mão na massa, uma pequena explicação sobre algumas operações (tidyverse)
4 Processamento de dados
Faremos o download dos dados das eleições pelo pacote cepespR. Nele teremos a cada municipio do Rio de Janeiro, dois valores: Total de votos para o candidato do PT (Fernando Haddad) e o total de votos ao candidato do PSL ().
Vamos filtrar para termos os dados do segundo turno, apenas. Além disso, precisaremos fazer alguns processamentos para poder trabalhar com o percentual de votos. Para isso usaremos duas funções muito importantes e úteis: group_by() e summarise():
4 Processamento de dados
group_by()
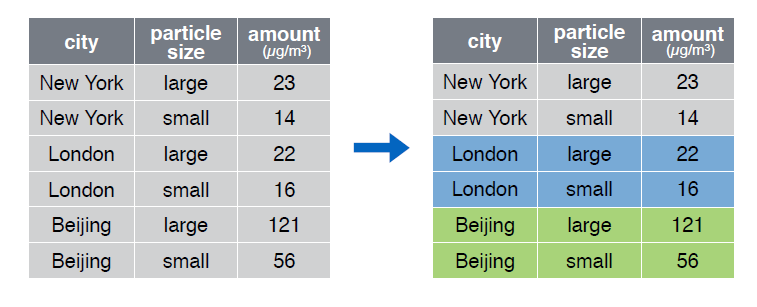
4 Processamento de dados
summarise()
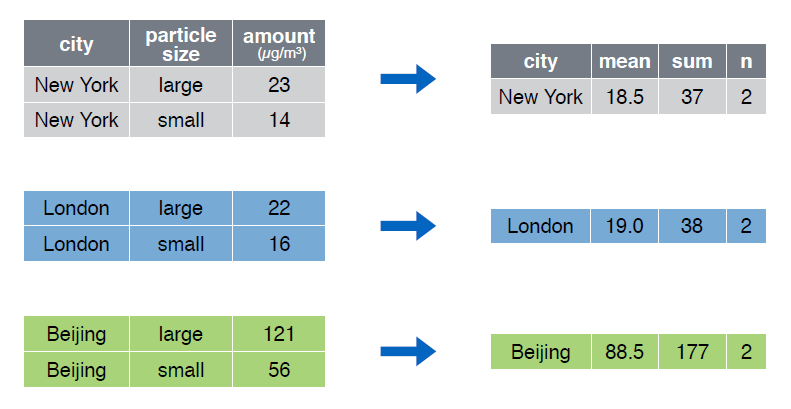
Essas funoes serão usadas para calcular o total de votos válidos de cada município e, em seguida, calcular o percentuald e votos a cada candidato.
Mão na massa!!!
O Pulo do gato
O Pulo do gato
O que é de fato o Moran I?
pt <- municipios %>% group_by(code_muni) %>% filter(NUMERO_CANDIDATO == 13)nb <- poly2nb(pt, queen=TRUE, row.names = pt$name_muni) lw <- nb2listw(nb, style="W", zero.policy=TRUE) pt$lag <- lag.listw(lw, pt$perc_vote)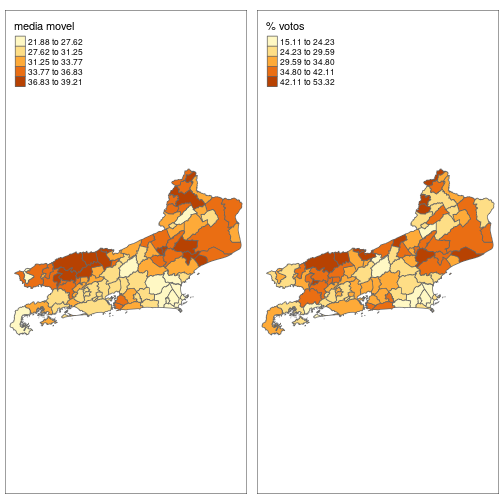
O Pulo do gato
plot(pt$lag, pt$perc_vote)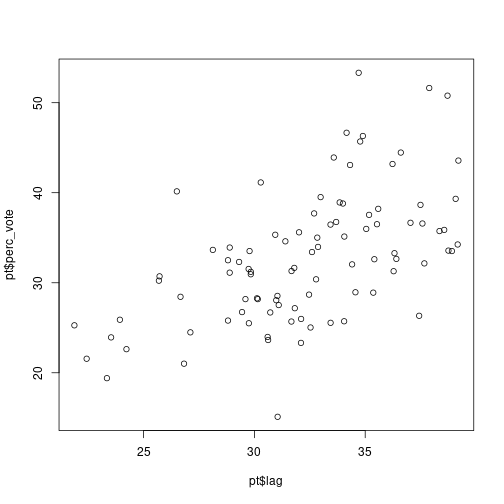
O Pulo do gato
regressao <- lm(pt$lag ~pt$perc_vote)#summary(regressao)coef( regressao )## (Intercept) pt$perc_vote ## 21.8277936 0.3203159moran.test(pt$perc_vote, lw)## ## Moran I test under randomisation## ## data: pt$perc_vote ## weights: lw ## ## Moran I statistic standard deviate = 4.7248, p-value = 1.151e-06## alternative hypothesis: greater## sample estimates:## Moran I statistic Expectation Variance ## 0.320315942 -0.010989011 0.004916791Script para essa live
https://gitlab.com/geocastbrasil/liver/-/blob/master/static/werlive13/werlive13.R
Considerações finais (5 min)
Considerações finais (5 min)
Próxima Live (25/08):
We R Live 14: Live com professor Jorge Kazuo Yamamoto

Maurício Vancine
mauricio.vancine@gmail.com
@mauriciovancine
@mauriciovancine
mauriciovancine.netlify.com
Felipe Sodré M. Barros
felipe.b4rros@gmail.com
@FelipeSMBarros
@felipe.b4rros
Geo Independência
Slides criados via pacote xaringan e tema Metropolis
 Fonte:
Fonte: